Основные понятия и характеристики спектрального прибора

Posted on 10.06.202411.06.2024 by Артем Аллилуев

Дифракционная решетка

В спектральных приборах для пространственного разложения света в спектр используются дифракционные решетки. Дифракционная решетка – это оптический элемент, состоящий из большого числа регулярно расположенных штрихов, нанесенных на плоскую или вогнутую поверхность. Решетки могут быть прозрачными или отражательными. Кроме того, различают амплитудные и фазовые дифракционные решетки. У первых периодически изменяется коэффициент отражения, что вызывает изменение амплитуды падающей волны. У фазовых дифракционных решеток штрихам придается специальная форма, которая периодически изменяет фазу световой волны. Наибольшее распространение получила плоская отражательная фазовая дифракционная решетка с треугольным профилем штрихов – эшелетт.

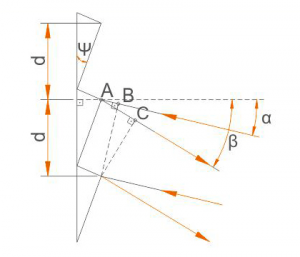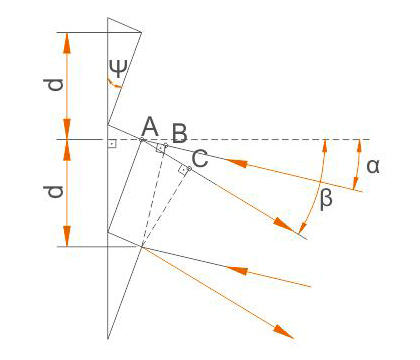
Рис.1. Пояснение принципа действия дифракционной решетки.

Длина волны блеска

Отражательная способность дифракционных решеток зависит от угла наклона штрихов – изменяя угол наклона грани штриха можно совместить центр дифракционного максимума функции $\bm{I_D}$ с интерференционным главным максимумом функции $\bm{I_N}$ любого порядка. Направление на центр дифракционного максимума определяется зеркальным отражением падающего пучка не от плоскости решетки, а от грани штриха. Таким образом, условие такого совмещения: углы $\bm{\alpha}$ и $\bm{\beta_{max}}$ должны одновременно удовлетворять соотношениям:

(1)

При этих условиях спектр данного порядка будет иметь наибольшую интенсивность. Угол $\bm{\beta_{max}}$ называют углом «блеска», а длину волны – длиной волны «блеска» $\bm{\lambda_{Blaze}}$ . Если область спектра для проведения исследований известна, то $\bm{\lambda_{Blaze}}$ может быть определена из соотношения:

(2)

где $\bm{\lambda_1}$ и $\bm{\lambda_2}$ – граничные длины волн диапазона спектра. Соотношение (2) помогает правильно выбрать решетку.

Пример 1. Исследуемый диапазон 400…1200 нм, т.е. $\bm{\lambda_1 =}$ 400 нм, $\bm{\lambda_2 =}$ 1200 нм. Тогда из формулы (2): $\bm{\lambda_{Blaze} =}$ 600 нм. Выберите решетку с блеском 600 нм.

Пример 2. Исследуемый диапазон 600…1100 нм. Расчет по формуле (2) дает с округлением 776 нм. Решетки с таким блеском в предлагаемом списке нет. Выбирается решетка с блеском, ближайшим к найденному, т.е. 750 нм.

Область энергетической эффективности дифракционной решетки

Область, где коэффициент отражения решетки не менее 0.405, называется областью энергетической эффективности:

(3)

Величина $\bm{ \Delta \lambda_E }$ зависит от порядка спектра: максимальна в первом порядке и быстро падает в спектрах более высоких порядков. Для первого порядка: $\bm{ \Delta \lambda_E = \frac{4}{3} \cdot \lambda_{Blaze} }$ . Длины волн, ограничивающие эту область: $\bm{ \lambda_1 = \frac{2}{3} \cdot \lambda_{Blaze} }$ и $\bm{ \lambda_2 = 2 \cdot \lambda_{Blaze} }$ .

Область дисперсии

Область дисперсии – спектральный интервал, в котором спектр данного порядка не перекрывается спектрами соседних порядков. Следовательно, имеет место однозначная связь между углом дифракции и длиной волны. Область дисперсии определяется из условия: $\bm{ k \cdot \lambda_2 = (k+1) \cdot \lambda_1 }$ .

(4)

Для первого порядка $\bm{ \Delta \lambda_D = \lambda_1 }$ , а $\bm{ \lambda_2 = 2 \cdot \lambda_1 }$ , т.е. область дисперсии охватывает интервал в одну октаву. Чтобы совместить область дисперсии с областью энергетической эффективности дифракционной решетки, необходимо чтобы выполнялось условие:

(5)

В этом случае в пределах области дисперсии коэффициент отражения решетки для $\bm{k = 1}$ будет не менее 0.68.

Пример. Если $\bm{\lambda_{Blaze} = }$ 600 нм, тогда $\bm{ \lambda_1 = \frac{3}{4} \cdot \lambda_{Blaze} = }$ 450 нм, а $\bm{ \lambda_2 = \frac{3}{2} \cdot \lambda_{Blaze} = }$ 900 нм. Таким образом, для данной дифракционной решетки в диапазоне от 450 нм до 900 нм область дисперсии совмещена с областью энергетической эффективности.

Дисперсия

Степень пространственного разделения лучей с разной длиной волны характеризует угловая дисперсия. Выражение для угловой дисперсии получим, дифференцируя уравнение для решетки:

(6)

Из этого выражения следует, что угловая дисперсия определяется исключительно углами $\bm{\alpha}$ и $\bm{\beta}$ , но не числом штрихов. В применении к спектральным приборам используется обратная линейная дисперсия $\bm{\frac{ d \lambda }{ d x }}$ , которая определяется как обратная величина произведения угловой дисперсии на фокусное расстояние: $\bm{ \frac{ d \lambda }{ d x } = \frac{ d \cdot \cos{ \beta } }{ k \cdot f }}.$

Разрешающая способность

Теоретическая разрешающая способность: $\bm{ R = \frac{ \lambda }{ \delta \lambda }}$ , где $\bm{\delta \lambda}$ – разрешение. Разрешающая способность дифракционной решетки как любого спектрального прибора определяется спектральной шириной аппаратной функции $\bm{\delta \lambda}$ . Для решетки шириной аппаратной функции является ширина главных максимумов интерференционной функции: $\bm{ \delta \lambda = \frac{ \lambda }{ k \cdot N }}$ . Тогда:

(7)

Спектральная разрешающая способность дифракционной решетки равна произведению порядка дифракции $\bm{k}$ на полное число штрихов $\bm{N}$ . Используя уравнение решетки:

(8)

где произведение $\bm{N \cdot d}$ – длина заштрихованной части решетки. Из выражения (8) видно, что при заданных углах $\bm{\alpha}$ и $\bm{\beta}$ величина $\bm{R}$ может быть увеличена только за счет увеличения размеров дифракционной решетки. Выражение для разрешающей способности может быть представлено в другом виде из (6) и (8):

(9)

где $\bm{ N \cdot d \cdot \cos{ \beta } }$ – ширина дифрагированного пучка, $\bm{ \frac{ d \beta }{ d \lambda } }$ – угловая дисперсия. Выражение (9) показывает, что разрешающая способность прямо пропорциональна величине угловой дисперсии.

Спектральная область решетки в зависимости от числа штрихов

Для каждой дифракционной решетки с периодом $\bm{d}$ существует предельная максимальная длина волны $\bm{\lambda_{\textbf{\textit{Max}}}}$ . Она определяется из уравнения решетки при $\bm{k=1}$ и $\bm{ \alpha = \beta = 90^{\circ}}$ и равна $\bm{ \lambda_{\textbf{\textit{Max}}} = 2 \cdot d}$ .

Поэтому при работе в различных областях спектра используются решетки с различным числом штрихов:

для УФ области: 3600 — 1200 штр/мм;
для видимой области: 1200 — 600 штр/мм;
для ИК области: менее 300 штр/мм.

Источник: “Характеристики спектрального прибора.” Sol Instruments

Каталог